Equação do 1º grau

3 – Equação do 1° grau 

A palavra equação vem do latim, “equa” cujo significa “igual”.

A equação de 1° grau é toda sentença aberta, em x, que se pode reduzir ao tipo ax + b = 0, com a ∈R^* e b∈ R. 

Resolução 

Notamos que ax + b = 0 ⇔ ax = – b ⇔ x = -b/a para a ≠0, concluímos que o conjunto-verdade da equação é V = {- b/a} 

Discussão 

Observando atentamente a equação ax + b= 0, com a, b ∈R, temos as circunstância: 

Para a ≠0, ax + b = 0 ⇔
(a equação admite apenas uma solução) 

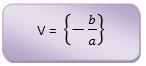
b) Para a = 0 e b ≠ 0, ax + b = 0 não tem solução, pois a sentença 0 . x + b = 0, com b ≠ 0 é sempre falsa. 

Sendo assim: 

c) Para a = 0 e b = 0, a equação ax + b = 0 aceita todos os números reais como solução, pois a sentença 0 . x + 0 = 0 é sempre verdadeira. 

Sendo assim: 

Observações: 

Sentenças abertas redutíveis ao tipo 0x = 0 são chamadas identidades.
(x + 1)² = x² + 2x + 1 é um exemplo de identidade em R.