4. Teorema da decomposição

Teorema

Qualquer função polinomial de grau restritamente positivo F(x) = a0xn + a1xn – 1 + a2xn – 2 +… + an – 1 x + an, sendo a0 ≠ 0, poderá ser decomposta e fatorada na forma:

F(x) = a0. (x – r1). (x – r2) . … . (x – rn)

Onde r1, r2, …, rn são as raízes de F.

Com exceção da ordem dos fatores, a unicidade desta decomposição é garantida.

Demonstração

O F.T.A. garante que a equação F(x) = 0 tem pelo menos uma raiz. Considerando r1 a raiz de F, nesse caso, conforme o teorema de D’Alembert, F é divisível por x – r1. Portanto: 

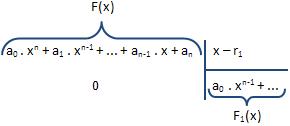
Logo, podemos representar assim:

F(x) = (r – r1) . F1 (x) (I) 

onde F1 é uma função polinomial que apresenta grau n-1 e coeficiente inicial a0.
Sendo n = 1 o teorema está demonstrado, pois F1 (x) = a0 e de (I) decorre F(x) = a0. (x – r1).

Sendo n > 1, nesse caso n – 1 > 0 e a equação F1 (x) = 0 possui, conforme o T.F.A., pelo menos uma raiz r2. Se r2 for a raiz F1 então esta função polinomial será divisível por x – r2. Portanto: 

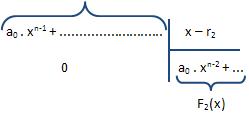
e assim F1 (x) = (x – r2) . F2(x).

Fazendo a substituição deste valor de F1 (x) em (I), temos:

F(x) = (x – r1) . (x – r2) . F2(x) (II) 

onde F2 é uma função polinomial que apresenta grau n – 2 e coeficiente inicial a0.

Sendo n = 2 o teorema está demonstrado, pois F2(x) = a0 e de (II) decorre F(x) = a0(x – r1) (x – r2)
Sendo n > 2, nesse caso n – 2 > 0 e a equação F2(x) = 0 possui, conforme o T.F.A., pelo menos uma raiz r3, e assim sucessivamente.

Depois de n aplicações contínuas do T.F.A., chegamos à F(x) = (x – r1) . (x – r2) . … . (x – rn) . Fn(x), onde Fn é uma função polinomial que apresenta grau n – 0 = 0 e coeficiente inicial a0.

Portanto Fn(x) = a0, e logo:

F(x) = a0 . ( x – r1) . (x – r2) . … . (x – rn)