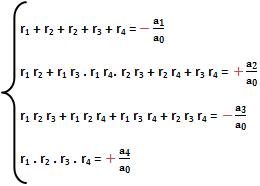5. Relações de Girard
Considere a função polinomial
F(x) = a0. xn + a1. xn – 1 + a2. xn – 2 +… + an – 1. x + an, sendo a0 ≠ 0 e n ≥ 1.
Considerando o teorema da decomposição podemos representar F(x) = a0 . (x – r1) . (x – r2) . … . (x – rn).
Empregando a propriedade distributiva, tornando redutíveis os termos semelhantes, e ordenando o polinômio, temos:
F(x) = a0 . xn – a0(r1 + r2 + … + rn) . xn-1 + a0 (r1r2 + r1r3 + …) xn-2 + …
Se igualarmos os coeficientes deste último polinômio, dois a dois, respectivamente, como os coeficientes iniciais a0, a1, a2, …, an, obtemos n relações entre as raízes e os coeficientes de F, tais relações são denominadas Relações de Girard, e são as seguintes:

Relações de Girard para uma equação de grau 2
A equação a0x2 + a1 x + a2 = 0 possue como raízes os termos r1 e r2, nesse caso:
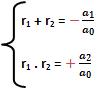
Relações de Girard para uma equação de grau 3
A equação a0x3 + a1x2 + a2x + a3 = 0 possui como raízes os termos r1, r2 e r3, nesse caso:
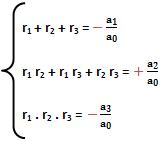
Relações de Girard para uma equação de grau 4
A equação a0x4 + a1x3 + a2x2 + a3x + a4 = 0 possui como raízes os termos r1, r2, r3 e r4, nesse caso: