2. Redução á forma F(x) = 0
Propriedades
1) Independente de qual for a função polinomial A, a equação algébrica P(x) = Q(x) será sempre equivalente à equação P(x) + A(x) = Q(x) + A(x).
Isto significa que: é possível transpor um termo de um membro para outro, substituindo o sinal do coeficiente, sem alterar o conjunto-solução.
2) Independente de qual for k ∈ C*, a equação algébrica P(x) = Q(x) sempre será equivalente à equação k . P(x) = k . Q(x).
Isto significa que: é possível multiplicar ambos os membros de uma equação por um número, que seja diferente de zero, sem modificar o seu conjunto-solução.
Redução
Considerando as propriedades acima, podemos concluir que qualquer equação algébrica P(x) = Q(x) pode ser reduzida à forma F(x) = 0, onde F é uma função polinomial. Portanto, qualquer equação algébrica pode ser passada para a forma:
F(x) = a0 xn + a1 xn-1 + a2 xn-2 + … + an-1 x + an = 0
Por esta redução podemos considerar as seguintes situações:
1) F(x) ≡ 0
Esta equação é do tipo 0 . xn + 0 . xn-1 + … + 0 . x + 0 = 0, e é uma sentença verdadeira seja qual for x complexo.
Portanto: V = C
2) F(x) = k ≠ 0
Esta equação é do tipo 0 . xn + 0 . xn-1 + … + 0 . x + k = 0, e é uma sentença falsa, seja qual for x complexo.
Portanto: V = ∅
3) F(x) = ax + b com a ≠ 0
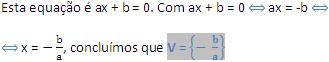
4) F(x) = ax2 + bx + c com a ≠ 0

5) gr(F) = 3 ou gr(F) = 4
As raízes das equações do terceiro e do quarto grau também podem ser obtidas através de fórmulas gerais, porém tais fórmulas são muito mais difíceis.
6) gr(F) > 4
Não há fórmulas resolutivas para equações de grau maior de quatro.