Raízes reais

10. Raízes reais

Teorema de Bolzano

Considere F como função polinomial de coeficientes reais e {x₁; x₂} ⊂ R, sendo x₁ < x₂. Quando F(x₁) . F(x₂) ≤ 0, nesse caso a equação F(x) = 0 terá pelo menos uma raiz real r, tal que r ∈ [x₁; x₂].

Exemplos:

Nos gráficos abaixo, a equação F(x) = 0 no intervalo [x₁; x₂], possui:

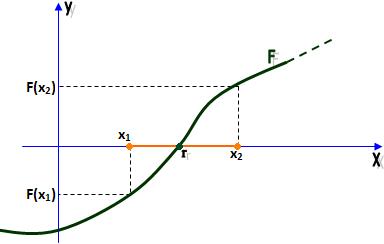
1) Uma raiz real.

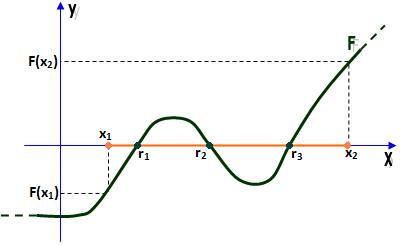
2) Três raízes reais distintas 

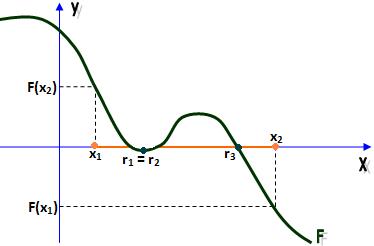
3) Uma raiz dupla e outra simples. 

4) Uma raiz real tripla.

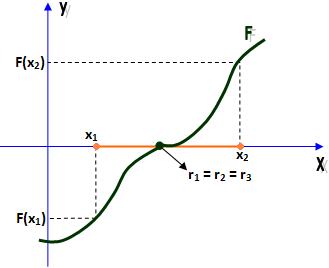
Observação:

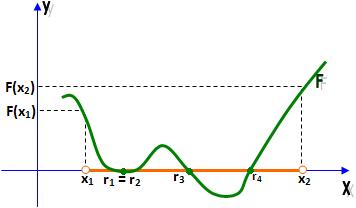
Com F(x₁). F(x₂) > 0, a equação F(x) = 0 pode ou não possuir raízes reais no intervalo ]x₁; x₂[. 

Nos gráficos abaixo, resulta-se que na equação F(x) = 0 no intervalo ]x₁; x₂ [ há: 

a) duas raízes reais distintas.

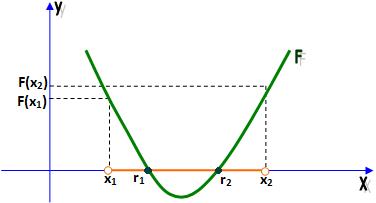
b) raiz real inexistente 

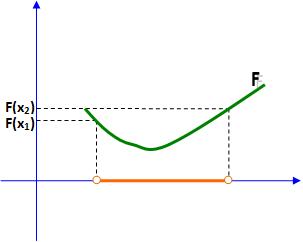
c) quatro raízes reais distintas: 

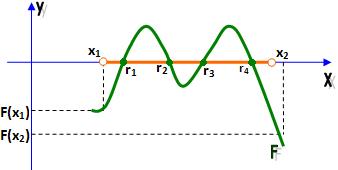
d) uma raiz real dupla e duas raízes reais simples