Raízes racionais
Por Redação
8. Raízes racionais
Teorema Considerando o número racional ![]() , sendo p e q primos entre si, como a raiz da equação a0 . xn + a1 . xn-1 + … + an-1 . x + an = 0, sendo a0 ≠ 0 e coeficientes inteiros, nesse caso p é divisor de an e q é divisor de a0.
, sendo p e q primos entre si, como a raiz da equação a0 . xn + a1 . xn-1 + … + an-1 . x + an = 0, sendo a0 ≠ 0 e coeficientes inteiros, nesse caso p é divisor de an e q é divisor de a0.
Demonstração
Considerando ![]() como a raiz da equação, nesse caso, temos:
como a raiz da equação, nesse caso, temos:

Isolando o termo a0 . pn, na igualdade acima, é possível evidenciar q; da mesma forma, isolando an . qn é possível evidenciar p.
Portanto:
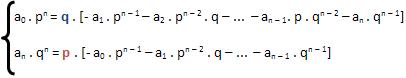
Considerando:
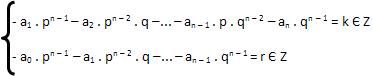
Temos:

Conseqüências:
1) Quando a equação a0 . xn + a1 . xn-1 + … + an-1 . x + an = 0, de coeficientes inteiros, admite uma raiz inteira p, nesse caso p será divisor de an.
2) Qualquer raiz racional da equação 1 . xn + a1 . xn-1 +
+ … + an-1 . x + an = 0, de coeficientes inteiros, é obrigatoriamente inteira.
