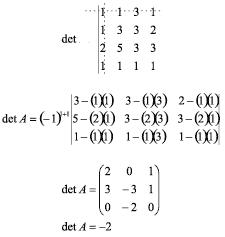Teorema de Laplace
Por Redação
Teorema de LAPLACE
O determinante de uma matriz quadrada de ordem 2 é igual à soma dos produtos dos elementos de uma fila qualquer pelos respectivos co-fatores.
Aplicação
Calcule
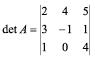
Procedimentos
I. Escolhe-se uma fila qualquer do determinante:
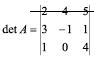
II. Coloca-se o sinal correspondente à potência (-1)i+j, do cálculo do co-fator, em cima dos elementos da fila selecionada:
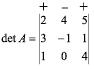
III. Multiplica-se cada elemento da fila selecionada, com o sinal do co-fator, pelo seu menor complementar.
det A = a11A11 + a12A12 + a13A13
Regra de CHIÓ
Para calcular o determinante de uma matriz de ordem n > 3 é necessário abaixar a ordem. Uma das maneiras é usar o Teorema de Laplace. Existe, além disso, uma regra prática dada por Chió que consiste em:
1.º Escolher um elemento aij = 1 (caso não exista, aplicar as propriedades para que apareça o elemento 1).
2.º Suprimir a linha (i) e a coluna (j) do elemento aij = 1, obtendo-se o menor complementar do referido elemento.
3.º Subtrair de cada elemento do menor complementar obtido o produto dos elementos que ficam nos pés das perpendiculares traçadas do elemento considerado às filas suprimidas.
4.º Multiplicar o determinante obtido no 3.º item por (-1)i+j onde i e j designam as ordens da linha e da coluna às quais pertence o elemento aij = 1.
Exemplo: