12 – Propriedades complementares
a) Teorema de Binet
Considerando A e B como matrizes quadradas de mesma ordem, temos:

Existem duas formas para calcular o determinante do produto de duas matrizes quadradas A e B de mesma ordem:
a) obter o produto de A . B das duas matrizes e calcular o determinante dessa matriz.
b) calcular os determinantes de A e de B separados e multiplicar os dois valores obtidos (Teorema de Binet).
c) Determinante de Vandermonde.

A matriz acima é denominada matriz de Vandermonde ou matriz de potências da linha (a1, a2, a3, …, an).
Nesse tipo de matriz o determinante é igual ao produto de todas as diferenças possíveis entre um elemento qualquer da linha (a1, a2, a3, …, an) e todos os anteriores. Representando o produto com o símbolo π:
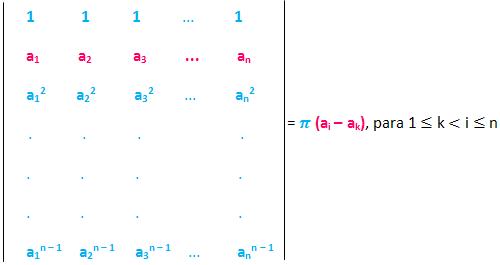
Exemplo:
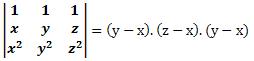
d) Soma de determinantes
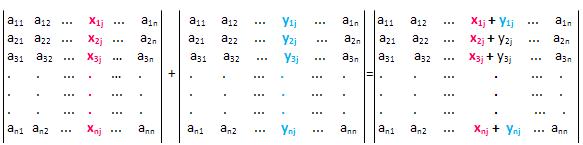
Exemplo:

e) Zeros num dos lados da diagonal principal
Em uma matriz quadrada de ordem n, todos os elementos dispostos na mesma face da diagonal principal são nulos, nesse caso seu determinante será igual ao produto dos elementos dessa diagonal.
Exemplo:
f) Zeros num dos lados da diagonal secundária
Em uma matriz quadrada de ordem n, todos os elementos dispostos na mesma face da diagonal secundária são nulos, neste caso, o seu determinante será igual ao produto dos elementos dessa diagonal, multiplicado por
1° Exemplo:
Obs. A diagonal principal de uma matriz é aquela que junta o canto superior esquerdo com o canto inferior direito. E a diagonal secundária de uma matriz é aquela que junta o canto superior direito como a canto inferior e esquerdo.