Equação de uma curva
Dizemos que uma equação nas variáveis x e y é a equação de uma curva λ se, e somente se:
– as coordenadas de todos os pontos de λ satisfazem a equação.
– todo par (x; y) solução da equação representa um ponto da curva λ.
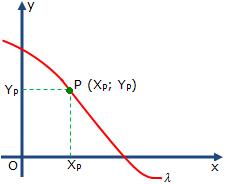
Observe que, se o ponto P(xP; yP) pertence a λ, suas coordenadas xp e yp satisfazem a equação de λ.
Interceptos de uma curva
Interceptos de uma curva são os pontos em que a curva corta o eixo cartesiano.
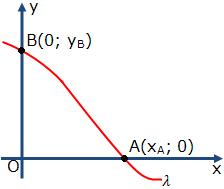
Na figura acima, o ponto A(xA; 0) é o intercepto no eixo 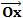
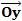
Intersecção de curvas
Considere λ1 e λ2 como duas curvas planas de equações s1 e s2, respectivamente.
Dizemos que todo ponto P é a intersecção de λ1 e λ2, tal que P pertença, simultaneamente, às duas curvas λ1 e λ2 e, portanto, satisfaça as equações s1 e s2.
Desse modo:
