Coordenadas cartesianas na reta
Definições
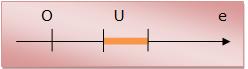
I) Eixo cartesiano
Toda reta orientada, com uma base estável e com um segmento adotado como unitário é denominado Eixo cartesiano.
(o) = origem
(U) = unidade
(e) = eixo
II) Medida Algébrica
A medida algébrica de um segmento orientado entre o eixo (e) é um número verdadeiro, do qual o módulo representa o tamanho do segmento e cujo sinal seja positivo ou negativo, assim como o sentido do segmento concorde ou discorde do sentido de eixo:
Vejamos o exemplo:
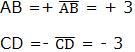

III) Abscissa
(e) representa o eixo cartesiano.
A cada ponto P de e equivale a um único número verdadeiro xp e mutuamente. Desta forma:
“Há uma aplicação bijetora entre o conjunto dos números reais e o conjunto dos pontos de eixo cartesiano e”.
Circunstancialmente:
“A abscissa de um ponto P sobre um eixo cartesiano e é o número verdadeiro xp que a ele corresponde.

Na representação:
P (Xp) ………. abscissa de P é XP.
A (XA)………. abscissa de A é XA.
Note que a abscissa de um ponto de um eixo é na verdade a medição algébrica do segmento 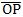
A base separa o eixo em dois grupos de pontos: Abscissas positivas e negativas.
Medida algébrica de um segmento orientado
Sendo as abscissas de pontos A e B de e, determinaremos o calculo algébrico (AB) do segmento orientado
Considerando A (XA) e B (XB), a Relação de Chasles, temos:
OA + AB + BO = 0 ⇔ OA + AB – OB = 0 AB = OB – OA
Assim: AB = XB – XA