Números racionais e números irracionais
Por Redação
5. Números racionais e números irracionais
O conjunto Q
O conjunto de números racionais é representado pela Q.
Podemos considerar um número real x como racional se houverem números inteiros a e b, sendo b ≠ 0, onde ![]() .
.
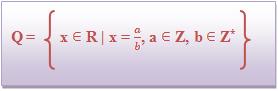
Teorema

Conseqüência
Os números não exatos não periódicos são os únicos números que não são racionais.
O conjunto R – Q
O conjunto de números irracionais é simbolizado por R – Q.
Podemos considerar um número real x como irracional quando x não é racional.

Logicamente:
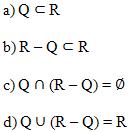
Estrutura de Q
Considerando ![]() como números racionais, estão determinadas em Q:
como números racionais, estão determinadas em Q:
a) a igualdade: ![]()
b) a adição: ![]()
c) a multiplicação: ![]()
d) a relação de ordem: ![]()
Propriedades do fechamento
1) Q é fechado para as quatro operações fundamentais da matemática, portanto, a soma, a diferença, o produto e o quociente de dois números racionais também será racional.
2) R – Q não é fechado para as quatro operações fundamentais da matemática, portanto a soma a diferença, o produto e o quociente de dois números irracionais pode não ser irracional.
Conclusão:
Considerando a e b como números racionais, e x e y como números irracionais, podemos estabelecer que:
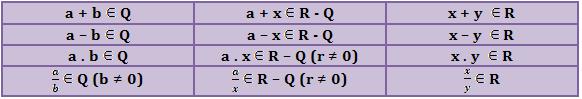
Radical duplo
Sabendo que x e y são números naturais onde ![]() , logo:
, logo:
![]()
