Números inteiros
Por Redação
2. Números inteiros
O conjunto Z
O conjunto dos números inteiros é simbolizado pela letra maiúscula Z.
Os números inteiros são: -3, -2, -1, 0, 1, 2, 3,…

Estrutura de Z
Assim como em N, nos números inteiros Z também estão determinadas as duas operações: adição e multiplicação. E as propriedades de N são equivalentes para Z.
Observação: qualquer número inteiro possui um número oposto: 1 –> – 1.
Múltiplo e divisor em Z
1) Considere a e b como dois números inteiros. Sabemos que b é divisor de a e que a é múltiplo de b apenas quando existe c inteiro onde a = b . c.
Portanto, sendo a, b e c números inteiros, temos:

2) Sendo o conjunto dos múltiplos do número inteiro a representado por D(a), temos:
![]()
3) Sendo o conjunto de múltiplos do número inteiro a representado por M(a), temos:
![]()
Exemplos:
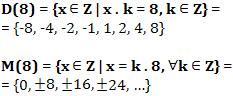
Propriedade de D(a)
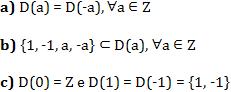
Propriedades de M(a)
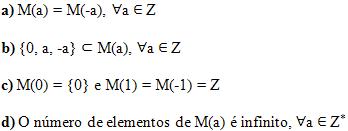
Número par e número impar
1) Um número inteiro a será par somente quando este for múltiplo de 2.
2) Um número inteiro a será ímpar somente quando este não for múltiplo de 2.
3) No caso de ![]() , logo:
, logo:
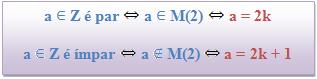
Número primo e numero composto
1) Um número inteiro p, sendo p ≠ 0, p ≠ 1 e p ≠ -1, será um número primo quando os números únicos divisores forem 1, -1, p e –p.
2) Um número inteiro a, sendo a ≠ 0, a ≠ 1 e a ≠ -1, será um número composto quando haver mais de 4 divisores.
Veja a representação:

Teorema fundamental da aritmética
Qualquer número composto pode sofrer uma decomposição e uma fatoração num produto de fatores primos. Com exceção da ordem dos fatores e do sinal dos fatores, essa decomposição será única.
Exemplo:
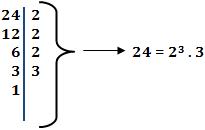
Número de elementos da D(a)

Maximo divisor comum (mdc)
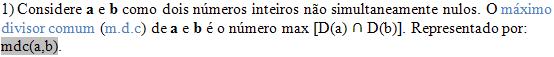
Veja a representação:
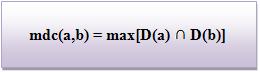

Mínimo múltiplo comum (mmc)
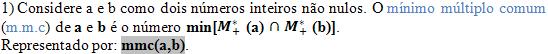
Veja a representação:

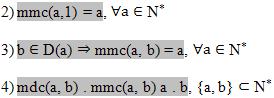
Números primos entre si
1) Os números inteiros a e b serão considerados de primos entre si apenas quando seus únicos divisores comuns forem 1 e -1.
Veja a representação:
![]()
2) Dois números inteiros consecutivos são primos entre si pois mdc(n, n + 1) = 1.
3) Dois números primos, distintos e não-simétricos são primos entre si.
4) Sendo ![]() , logo:
, logo:
![]()
Critérios de divisibilidade
Divisibilidade por 2
Um número é divisível por 2 se ele for par, ou seja, se terminar em 0, 2, 4, 6 ou 8.
Divisibilidade por 3
Um número é divisível por 3 se a soma de seus algarismos for divisível por 3.
Divisibilidade por 5
Um número é divisível por 5 se o algarismo das unidades for 0 ou 5.
Divisibilidade por 7
Para saber se um determinado número é divisível por 7, deve-se seguir os seguintes passos:
Considerar o último algarismo do número e o dobro deste algarismo deve ser subtraído dos outros números. Se o número obtido for divisível por 7, sabemos que o número inicial também é divisível por 7.
Exemplo:
315
5 x 2 = 10
10 – 31 = 21
21 é divisível por 7, então 315 também é divisível por 7.
Divisibilidade por 11
Um número é divisível por 11 se a soma dos algarismos de ordem par subtraída da soma dos algarismos de ordem ímpar for divisível por 11.
Exemplo:
Ordem par: 554829 –> 5 + 8 + 9 = 22
Ordem ímpar: 554829 –> 5 + 4 + 2 = 11
22 – 11 = 11
11 é divisível por 11, então 554829 também é divisível por 11.
