O que é Composição dos Movimentos
Por Redação
1. COMPOSIÇÃO DE MOVIMENTOS
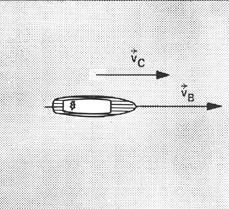
Um barco, navegando em um rio com correnteza, está animado de duas velocidades: a sua própria (![]() B), em relação à água (proporcionada pelos motores), e a da correnteza (
B), em relação à água (proporcionada pelos motores), e a da correnteza (![]() C), em relação à Terra, que também desloca o barco.
C), em relação à Terra, que também desloca o barco.
a) Com que velocidade o barco desce o rio?
– A velocidade é ![]() , resultante de
, resultante de![]() B e
B e![]() C (vetores de mesma direção e mesmo sentido). Então: v = vB + vC (o barco desce o rio mais rapidamente do que desceria se não existisse a correnteza).
C (vetores de mesma direção e mesmo sentido). Então: v = vB + vC (o barco desce o rio mais rapidamente do que desceria se não existisse a correnteza).
(a)
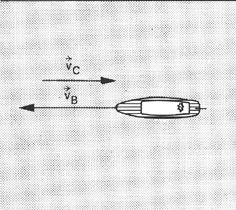
b) Qual a velocidade com que o barco sobe o rio?
– Agora,![]() B e
B e ![]() C têm a mesma direção, mas sentidos contrários. O módulo da velocidade resultante será: v = vB – vC (o barco gastará mais tempo para subir o rio do que para descer).
C têm a mesma direção, mas sentidos contrários. O módulo da velocidade resultante será: v = vB – vC (o barco gastará mais tempo para subir o rio do que para descer).
(b)
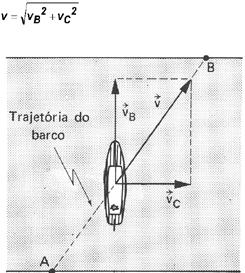
c) Se o barco for orientado perpendicularmente à margem, com que velocidade ele atravessa o rio?
– Neste caso, ![]() B e
B e ![]() C são ortogonais (perpendiculares) entre si. O barco deslocar-se-á na trajetória AB, como mostra a figura. O módulo da velocidade resultante será (pelo Teorema de Pitágoras):
C são ortogonais (perpendiculares) entre si. O barco deslocar-se-á na trajetória AB, como mostra a figura. O módulo da velocidade resultante será (pelo Teorema de Pitágoras):
(c)
velocidade do barco e a velocidade da correnteza são perpendiculares entre si, ![]() B não tem componente na direção de
B não tem componente na direção de![]() C, ou seja, a correnteza não terá nenhuma influência no tempo que o barco gasta para atravessar o rio; haja ou não correnteza o tempo de travessia será o mesmo, pois o efeito da correnteza é unicamente o de deslocar o barco rio abaixo. Do mesmo modo, sendo nula a componente de
C, ou seja, a correnteza não terá nenhuma influência no tempo que o barco gasta para atravessar o rio; haja ou não correnteza o tempo de travessia será o mesmo, pois o efeito da correnteza é unicamente o de deslocar o barco rio abaixo. Do mesmo modo, sendo nula a componente de ![]() B na direção da correnteza, a velocidade do barco não terá influência no seu movimento rio abaixo.
B na direção da correnteza, a velocidade do barco não terá influência no seu movimento rio abaixo.
Essa independência de dois movimentos simultâneos e perpendiculares foi enunciada por Galileu.
PRINCÍPIO DA INDEPENDÊNCIA DOS MOVIMENTOS SIMULTÂNEOS
Quando um corpo está animado, simultaneamente, por dois movimentos perpendiculares entre si, o deslocamento na direção de um deles é determinado apenas pela velocidade naquela direção.
Aplicações
01. Entre as cidades A e B existem sempre correntes de ar que vão de A para B com uma velocidade de 50km/h. Um avião, voando em linha reta, com uma velocidade de 150km/h, em relação ao ar, demora 4h para ir de B até A. Qual a distância entre as duas cidades?
Solução:
O vento sopra de A para B. O avião voa de B para A. Como as velocidades têm sentidos contrários, a velocidade resultante do avião é:
v = 150 – 50 = 100km/h
O avião percorre a distância entre as duas cidades em 4h. Então:
S = So + vt
S = 0 + 100 x 4 = 400km (a distância entre A e B).
