velocidade vetorial instantânea 

Quando o intervalo de tempo propende a zero, a velocidade vetorial média propende a um limte que é denominado velocidade vetorial instantânea. 

Podendo ser representada pela função:

                   →
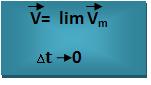
Módulo de V:

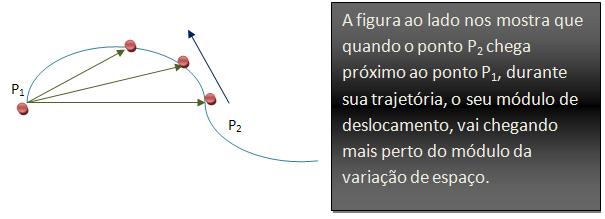
É importante lembrarmos que o módulo da velocidade vetorial instantânea, sempre será igual ao módulo da velocidade escalar instantânea. 
      

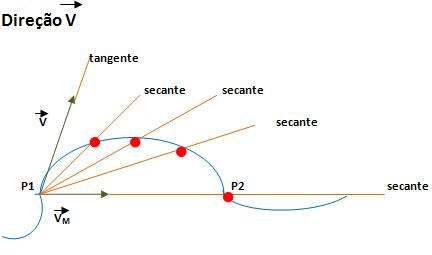
O desenho acima nos mostra que a velocidade vetorial média Vm tem sua direção representada por P1 e P2 sendo secante à trajetória, ou seja, conforme P2 propende para P1, a reta secante também propende para a reta tangente à trajetória em P1, isto é, a direção da velocidade vetorial instantânea é sempre tangente à trajetória.


                              →
Notação do vetor V 

Considerando que t, seja o versor da tangente à trajetória V a velocidade escalar, a velocidade vetorial instantânea passa a ser representada por:

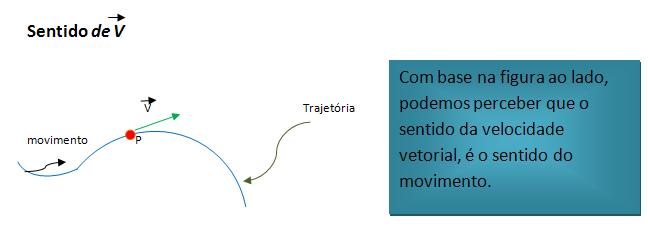
Essa função quer dizer que o módulo da velocidade vetorial instantânea é o mesmo que o da velocidade escalar, sua direção é a representada pela reta da tangente à trajetória, e o seu sentido é o do movimento do corpo, que é determinado pelo sinal da velocidade escalar V. 

É importante lembrarmos que a velocidade vetorial instantânea, pode ser chamada apenas de velocidade vetorial. 

Velocidade vetorial constante 

Podemos afirmar que a velocidade vetorial, será constante, quando o móvel do objeto, estiver em repouso, ou até mesmo em movimento retilíneo e uniforme. 

* Partícula em repouso: que é quando a velocidade vetorial é sempre nula. 
* Partícula em movimento retilíneo e uniforme: para que a velocidade vetorial seja constante e diferente de zero, ela deve ser constante em módulo, que é o movimento uniforme, e em orientação, que é a trajetória retilínea. 
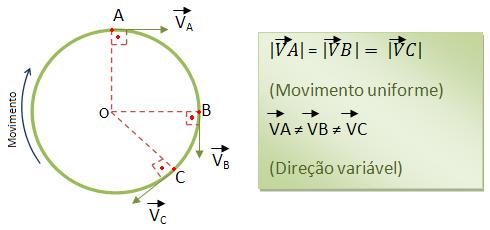
Considerando uma partícula em movimento circular e uniforme, com uma velocidade em módulo constante, e com direção variável, podemos dizer que ela será um vetor variável.