Componentes da aceleração vetorial
Estudo da aceleração tangencial
Aceleração tangencial (a t) – é o componente da aceleração vetorial na direção do vetor velocidade e indica a variação do módulo deste. Possui módulo igual ao da aceleração escalar:
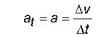
Módulo de at: O módulo da aceleração tangencial é totalmente igual ao valor absoluto da aceleração.
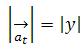
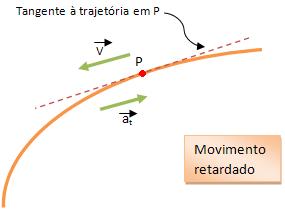
Direção de at: A direção da aceleração tangencial é paralela à velocidade vetorial, isto é, tangente à trajetória.
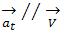
Sentido de at: o sentido irá depender do movimento, vejamos:
* Se o movimento for acelerado, consequentemente o módulo da sua velocidade irá aumentar e sua aceleração tangencial irá ter o mesmo sentido da velocidade vetorial.
Vejamos:
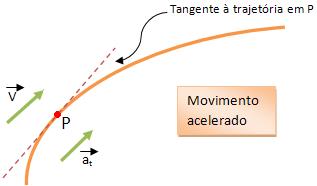
* Se o movimento for retardado, consequentemente o módulo da velocidade irá diminuir e sua aceleração tangencial irá ter o sentido oposto ao da velocidade vetorial. Vejamos:
Notação de at: é quando a grandeza vetorial é representada matematicamente.
Vejamos:
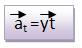
→
Efeito at
Podemos dizer que a aceleração escalar y, tem uma relação direta com a variação da velocidade escalar V, do módulo da velocidade vetorial V.
Propriedades:
1. Quando falamos de movimento uniforme, podemos dizer que a velocidade vetorial apresenta um módulo constante, e por isso sua aceleração tangencial é sempre nula, independente da sua trajetória.
2. Quando falamos de movimento não uniforme, podemos dizer que a velocidade vetorial apresenta um módulo variável, e por isso sua aceleração tangencial não será sempre nula.
3. Sempre que um corpo ou um objeto estiver em repouso, sua aceleração tangencial será nula.
4. No instante em que y = 0, a aceleração tangencial será nula, independente de o móvel estar em repouso ou em movimento.
Estudo da aceleração centrípeta
Aceleração centrípeta ou normal ( c) – é o componente da aceleração vetorial na direção do raio de curvatura (R) e indica a variação da direção do vetor velocidade ( ). Tem sentido apontando para o centro da trajetória (por isso, centrípeta) e módulo dado por:
Sendo que, V é a velocidade escalar e R é o raio de curvatura da trajetória.
Importante: nos movimentos retilíneos, c é nula porque o móvel não muda de direção nesses movimentos.
Direção de acp: A direção da aceleração centrípeta é considerada normal em relação à tangente à trajetória, ou seja, ela é igual a velocidade vetorial.
Vejamos:
Sentido de acp: O sentido da aceleração centrípeta sempre será voltado para o centro da circunferência, osculadora à trajetória, ou seja, direcionado para uma região convexa limitada pela curva.
Notação de acp: A função que podemos usar para representarmos a notação da aceleração centrípeta é:
Efeito de acp: Quando falamos de trajetória retilínea, podemos considerar
R ⇒ ∞ e acp= 0. Já quando falamos que a trajetória é curva, podemos dizer que a velocidade vetorial varia em direção e sua aceleração centrípeta nem sempre difere de zero.
Notas:
* Quando falamos de movimentos retilíneos, podemos dizer que a velocidade vetorial apresenta uma direção constante, e com isso, sua aceleração centrípeta se torna constantemente nula.
* Sempre que o móvel estiver em repouso, sua aceleração centrípeta, será nula.
Vejamos alguns exemplos: