ACELERAÇÃO VETORIAL INSTANTÂNEA

É a aceleração vetorial de um móvel em cada ponto de sua trajetória.

Como todo vetor pode ser obtido pela soma de suas componentes perpendiculares, vamos decompor o vetor aceleração instantânea, tomando como base a direção do vetor velocidade: 
       
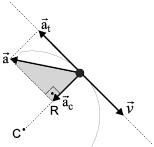
a) Aceleração tangencial (t) – É a componente da aceleração vetorial na direção do vetor velocidade ( ) e indica a variação do módulo deste. Possui módulo 

igual ao da aceleração escalar: 
   

Importante:
1) Em movimentos acelerados, t e têm o mesmo sentido.

2) Em movimentos retardados, t e têm sentidos contrários, como na figura anterior.

3) Em movimentos uniformes, t é nula, já que o módulo de não varia nesses movimentos.

b) Aceleração centrípeta ou normal (c) – É a componente da aceleração vetorial na direção do raio de curvatura (R) e indica a variação da direção do vetor velocidade (). Tem sentido apontando para o centro da trajetória (por isso, centrípeta) e módulo

dado por: 
       
Importante: nos movimentos retilíneos,c é nula porque o móvel não muda de direção nesses movimentos.

Aceleração vetorial resultante – A obtenção da intensidade da aceleração resultante pode ser feita aplicando-se o Teorema de Pitágoras no triângulo retângulo em destaque na figura:

a2 = a2t + a2c

Aplicações

01. (PUC–SP) Um móvel parte do repouso e percorre uma trajetória circular de raio 100m, em movimento acelerado

uniformemente, de aceleração escalar igual 1m/s2. Calcule, após 10s, as componentes tangencial e centrípeta da aceleração.

Solução:
 .