Cilindro

Conceito:

Consideremos um círculo de centro O e raio r num plano , e um segmento de reta , cuja reta suporte intercepta em Q. Temos segmentos de reta paralelos e congruentes a , cada um deles com uma das extremidades num ponto do círculo e a outra extremidade num mesmo semi-espaço dos determinados por ele. A reunião de todos esses segmentos é um sólido chamado cilindro.

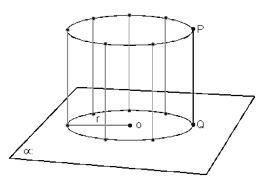
Elementos

Considerando o cilindro representado abaixo, temos:

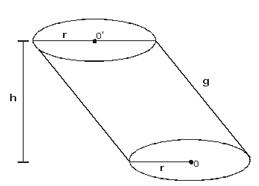
a) os círculos de centros O e O’ e o raio r situados em planos paralelos são as bases do cilindro;

b) os segmentos paralelos a OO com as extremidades em pontos das circunferências das bases são as geratrizes (g);

c) a reta OO «é o eixo do cilindro;

d) a distância entre os planos das bases é a altura (h) do cilindro.

Classificação

Um cilindro pode ser classificado conforme a inclinação da geratriz em relação aos planos das bases:

a) o cilindro circular é oblíquo quando a geratriz é oblíqua às bases;

b) o cilindro circular é reto quando a geratriz é perpendicular às bases.

As duas figuras anteriores são cilindros oblíquos, enquanto a figura ao lado representa um cilindro reto.
O cilindro circular reto é também chamado cilindro de revolução; ele é gerado pela rotação de um retângulo em torno de um de seus lados.

Áreas e Volumes

Área da Base: Ab

A área da base de um cilindro é a área de um círculo de raio r.

Ab = r2