Mínimo Múltiplo Comum (m.m.c)
Por Redação
Dois ou mais números sempre têm múltiplos comuns a eles.
Vamos achar os múltiplos comuns de 4 e 6:
Múltiplos de 6: 0, 6, 12, 18, 24, 30,…
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,…
Múltiplos comuns de 4 e 6: 0, 12, 24,…
Dentre estes múltiplos, diferentes de zero, 12 é o menor deles.
Chamamos o 12 de mínimo múltiplo comum de 4 e 6.
Indica-se: m.m.c (4 e 6) = 12
Agora vamos achar os múltiplos comuns de 40 e 60.
Múltiplos de 40: 0, 40, 80, 120, 160, 200, 240, 280, 320, 360, 400…
Múltiplo de 60: 0, 60, 120, 180, 240, 300, 360, 420, 480…
Os múltiplos comuns de 40 e 60 são: 0, 120, 360…
O número 120 é o menor ou mínimo múltiplo comum dos números naturais 40 e 60.
Indica-se: m.m.c (40 e 60) = 120.
Existem outras duas maneiras de calcular o m.m.c de dois ou mais números naturais:
Vamos começar determinando o menor número natural, diferente de zero, que é múltiplo comum dos números 20 e 40.
1º) Primeiramente, vamos decompor cada um dos números em fatores primos:
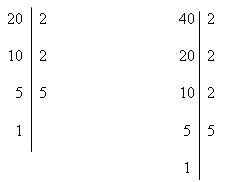
Agora, consideramos todos os fatores na forma fatorada, cada um deles com seu maior expoente.
Neste caso esses fatores são 23 x 5
O produto dos fatores encontrados será o m.m.c procurado, ou seja:
m.m.c (20, 40) = 23 x 5 = 40
2º) A outra maneira de calcular o m.m.c é fazendo uma decomposição simultânea, em fatores primos, considerando os mesmos números 20 e 40.
Neste processo decompomos todos os números ao mesmo tempo, num dispositivo como mostra o exemplo abaixo. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números.

ATIVIDADES
1) Calcule o m.m.c dos números abaixo e depois clique na alternativa correta:
a) 18 e 26
* 126 [R]
* 234 [R]
* 425 [R]
b) 24 e 36
* 72 [R]
* 48 [R]
* 66 [R]
c) 60, 80
* 320 [R]
* 260 [R]
* 240 [R]
d) 16 e 32
* 32 [R]
* 16 [R]
* 360 [R]
e) 50 e 75
* 175 [R]
* 150 [R]
* 75 [R]

 Mudanças provocadas pelo café
Mudanças provocadas pelo café