Tubos sonoros 

Ao soprar um tubo sonoro a coluna de ar vibra, havendo assim a produção de som.

Vejamos agora os tipos de tubos sonoros:

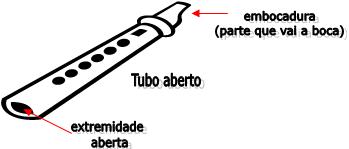
A) Abertos: os tubos abertos possuem uma extremidade oposta à embocadura, ou seja, a entrada do ar aberta. A onda estacionária se forma no ar de seu interior, quando o tubo aberto ressoa. 

Nas duas extremidades do tubo, ou seja, na embocadura e na extremidade aberta, há uma formação de ventres, isto é, uma interferência construtiva. 

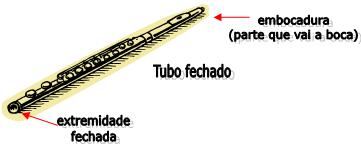
B) Fechados: Os tubos fechados possuem uma extremidade oposta a embocadura, ou seja, a entrada do ar fechada. A onda estacionária se forma no ar de seu interior, quando o tubo fechado ressoa. 

Podemos perceber que junto à embocadura, há formação de um ventre, ou seja, interferência construtiva, e junto à extremidade fechada, ocorre à formação de um nó, ou seja, interferência destrutiva. 

ondas estacionárias nos tubos

A) Tubos Abertos 

Vejamos uma figura abaixo, onde podemos perceber que estão representadas as três primeiras ondas estacionárias, que poderão aparecer na coluna de ar do interior de um tubo aberto que contenha um comprimento útil igual a L. Veremos abaixo os três modos de vibração que correspondem ao 1º, 2º e 3º harmônico. 

Vejamos: 

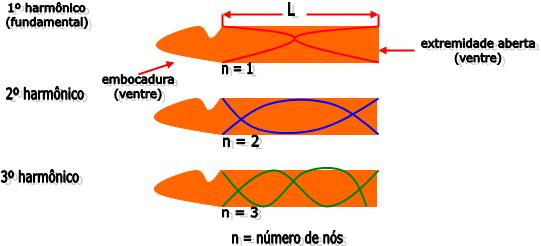
Considerando  o comprimento da onda estacionária que está presente no tubo, esse comprimento poderá ser expresso em função de L. Em cada caso é dado de uma forma, vejamos: 

Considerando V, como sendo o módulo da velocidade das ondas parciais, onde elas se superpõem para que haja formação das ondas estacionárias e fn, a freqüência de um harmônico de ordem n, vem:

B) Tubos fechados 

Vejamos uma figura abaixo, onde podemos perceber que estão representadas as três primeiras ondas estacionárias, que poderão aparecer na coluna de ar do interior de um tubo fechado que contenha um comprimento útil igual a L. Veremos abaixo os três modos de vibração que correspondem ao 1º, 2º e 5º harmônico. 

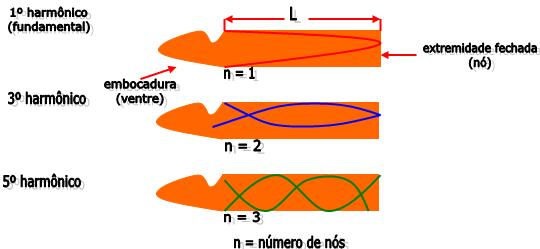
Considerando  o comprimento da onda estacionária que está presente no tubo, esse comprimento poderá ser expresso em função de L. Em cada caso é dado de uma forma, vejamos: 

Considerando V, como sendo o módulo da velocidade das ondas parciais, onde elas se superpõem para que haja formação das ondas estacionárias e f(2n – 1), a freqüência de um harmônico de ordem (2n -1), vem: